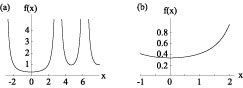
図1: $\disp f(x)=\frac{1}{\sin^2 x} - \frac{1}{x^2}$.
微分積分学I の受講生向けに,計算の検算方法をいくつか紹介しておく. 大学では,答えが簡単にはわからない問題に取り組むことが多い. 自分のやった計算について 「どこまで正しいか? 自分の力で確かめる技術」を習得しておくと, いろんな場面で役に立つだろう.
不定積分を求めたときは, 得られた答えを微分して もとの関数になるかどうか確かめる.
ついでに注意しておくと,有理関数の積分の場合は, 部分分数に分解するところで間違うことが多い. 例えば, 例2c の積分計算では, 式 \eqref{eq:ex1-1bunkai} を通分して 被積分関数のもとの形 $\dfrac{1}{(x^2-1)^3}$ になるかどうか 確認することも大事.
もしも複数の方法で計算できる場合は, 自分が初めに計算したのとは別の方法で計算してみて, 同じ答えが得られるかどうか確かめる.
例2a: $\displaystyle \lim_{x \to 0} \frac{1-\cos x}{x^2}$
この極限値は,例えば,次の3つの方法で計算できる.
$\cos x$ は, \[ \cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!} + \cdots \] と表すことができる (0を中心とするテイラー級数). これを分子に代入すると, \begin{eqnarray*} \frac{1-\cos x}{x^2} &=& \frac{1}{x^2} \left[ 1 - \left( 1 - \frac{x^2}{2} + \frac{x^4}{4!} + \cdots \right) \right] \\ &=& \frac{1}{x^2} \left( \frac{x^2}{2} - \frac{x^4}{4!} + \cdots \right) \\ &=& \frac{1}{2} - \frac{x^2}{4!} + (x^4, x^6, \cdots \;に比例する項) \end{eqnarray*} となる. $\disp \lim_{x \to 0} x^{2n}=0 \; (n=1, 2, \cdots)$なので, 極限値は$\dfrac{1}{2}$.
$y=\arctan \dfrac{x}{a}$ とおくと, $ \tan y = \dfrac{x}{a}$ である. この式の両辺を $x$ で微分すると, \[ \frac{dy}{dx} \frac{d}{dy} \tan y = \frac{1}{a}, \quad したがって,\quad \frac{1}{\cos^2 y} \frac{dy}{dx} = \frac{1}{a} \] を得る.これを整理すると, \[ \frac{dy}{dx} = \frac{1}{a} \cos^2 y = \frac{1}{a} \frac{1}{1 + \tan^2 y} = \frac{1}{a} \frac{1}{1 + (x/a)^2} = \frac{a}{a^2 + x^2} \] となる.
$y=\arctan \dfrac{x}{a}$ とおくと, $\tan y = \dfrac{x}{a}$ である. つまり,$x=a \tan y$ である. この式の両辺を$y$で微分すると, $\disp \frac{dx}{dy}=a \frac{d}{dy} \tan y = \frac{a}{\cos^2 y}$ である. 逆関数の微分法を使うと,次式を得る. \[ \frac{dy}{dx}=\frac{1}{\frac{dx}{dy}} =\frac{1}{\frac{a}{\cos^2 y}} =\frac{1}{a (1+\tan^2 y)} =\frac{1}{a [1+(x/a)^2]} =\frac{a}{a^2 + x^2}. \]
例2d: $\disp I=\int^2_{-1} f(x) dx$, $f(x)=\dfrac{1}{\sqrt{2+x-x^2}} =\dfrac{1}{\sqrt{-(x-2)(x+1)}} =\dfrac{1}{\sqrt{\frac{9}{4}-(x-\frac{1}{2})^2}}$.
この積分は,置換積分法で計算できる. 変数のおき方には例えば次の方法がある.
関数のグラフを正確に描くと極限値の検算ができることが多い.
例3a: $f(x)=\dfrac{1}{\sin^2 x}-\dfrac{1}{x^2}$ の極限値 $\disp \lim_{x \to 0} f(x)$.
$f(x)$ のグラフを図1に示す. $x=0$ 近くの拡大図 (図1(b)) から, $\disp \lim_{x \to 0} f(x)$ が 0.2 と 0.4 の間の値をとることがわかる. もっと細かい値を知りたければ,もっと拡大した図を描いてみればよい.

補足: この例題は,テイラー級数を利用すると楽に計算できる. ロピタルの定理を使っても計算できるけれど,微分計算がかなり面倒だ. ちなみに答えは $\frac{1}{3}$.
導関数の計算についても,グラフを描くことによって, その符号だけは検算できる.
例3b: $f(x)=x-\arctan(2x)$ の導関数は, $\disp f^\prime(x)=1-\frac{2}{(2x)^2+1}$ である.
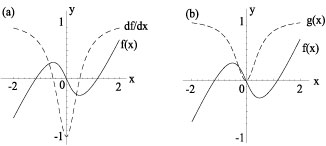
$y=f(x)$ と $y=f^\prime(x)$ を 重ねて描くと, 図2(a)のようになる. 両者を見比べると, $f(x)$ が増えているとき (減っているとき) $f^\prime(x)$ は正 (負) であることが確認できる. これで,$f^\prime(x)$ の符号だけは正しいことがわかる. もしも,計算を間違って,例えば $\disp f^\prime(x)=1-\frac{1}{(2x)^2+1}$ ($=g(x)$ とおく) としたらどうだろうか? 関数 $g(x)=1-\dfrac{1}{(2x)^2+1}$ の符号は $f(x)$ の増減と合わない [ 図2(b)参照 ]. したがって, $\disp f^\prime(x)=1-\frac{1}{(2x)^2+1}$ は間違いであることがわかる.
問題集,演習書,公式集などに, 自分の解いた問題と似たような問題が載ってないかどうか調べる. 図書館でいろんな本を漁ってみるとよいだろう.
数式処理ソフトは, 数式の展開・因数分解や微分積分などの演算をやってくれる. 次の使用例のように.
入力1: f=1/Sin[x]^2 - 1/x^2; <- fの定義.( ^2 は 2乗を意味する ) 入力2: Limit[f, x -> 0] <- 0における極限値を求めろ という命令 出力3: 1/3 <- 極限値 入力4: f = x - ArcTan[2 x]; <- fの定義 入力5: D[f, x] <- fをxで微分しろ という命令 出力6: 1 - 2/(1 + 4 x^2) <- 微分した結果 入力7: f = 1/Sqrt[2 + x - x^2]; <- fの定義.( Sqrt は 1/2乗を意味する ) 入力8: Integrate[f, x] <- fをxで積分しろ という命令 出力9: -ArcSin[1/3 (1 - 2 x)] <- 積分した結果
この例では,私が使っているソフト (Mathematica) での計算を紹介したが, 特にこのソフトを推奨している訳ではない (Mathematicaは有料のソフトで,しかもお安くはない). 無料で使える数式処理ソフトもある. 例えば,Maxima は無料で使える. MATLABも,鳥取大学の学生だったら無料で使える (ただし学内でないと使えないみたい.詳しくはメディアセンターで調べて下さい).
同じ問題を誰かに解いてもらって,自分の答えと比べる.
誰に聞く場合でも, その人の説明を鵜呑みにはしないこと. その人の言うことはどこまで正しいか? そして,自分にとってどこまで納得がいくか? といったことを,よく考えよう. 誰かの答えと自分の答えがくい違った場合は, どこから違いが生じたのか考えよう.
ついでに言っておくと,当然のことだが,私加藤も「誰か」の候補だ. 教員やTAへは,積極的に質問してほしい.