研究内容
荷電粒子運動や磁力線の軌道追跡などに用いる高精度数値積分アルゴリズムに関する研究
電磁場中での荷電粒子の運動を数値計算により追跡するときには,保存量を然るべく保存するアルゴリズムを用いることが重要である.例えば,惑星の運動を長時間追跡する際にエネルギー保存性の悪いアルゴリズムを用いると,離散化誤差の蓄積により,惑星は周回運動の中心にある天体に落下したり無限遠へ飛んで行ったりしてしまう.荷電粒子の場合にも,長時間の軌道を追う必要がある場面では,同様に保存性のよいアルゴリズムが必要となる.
これまで,天体力学や物性計算の分野では,ハミルトニアン分割(演算子分割)と漸化式による高次精度化を組み合わせ,高精度の軌道追跡アルゴリズムが開発されてきた.本研究では,これを荷電粒子の場合にも適用できるよう,非正準変数を用い,さらに時間変動する電磁場中でも使えるよう拡大相空間で定式化した.時間反転対称なアルゴリズムとなっている.数値計算の側面からは,ハミルトニアン分割というよりも,Poissonテンソルを分割すると捉えた方が理解しやすいことも指摘している.開発したアルゴリズムを用いて荷電粒子の軌道追跡を行い,その性能が理論通り得られることを示した.また,速く時間変動する電磁場中で,荷電粒子の振動中心が受けるponderomotive力による運動も適切に計算できることを示した.
上記の定式化は,Hamilton系なら共通して適用できるものである.その一例は磁力線の軌道であり,カオス的な振る舞いを示す磁力線の追跡へも適用を進めている.
M. Furukawa et al., Plasma Fusion Res. 11, 1303003 (2016)など.
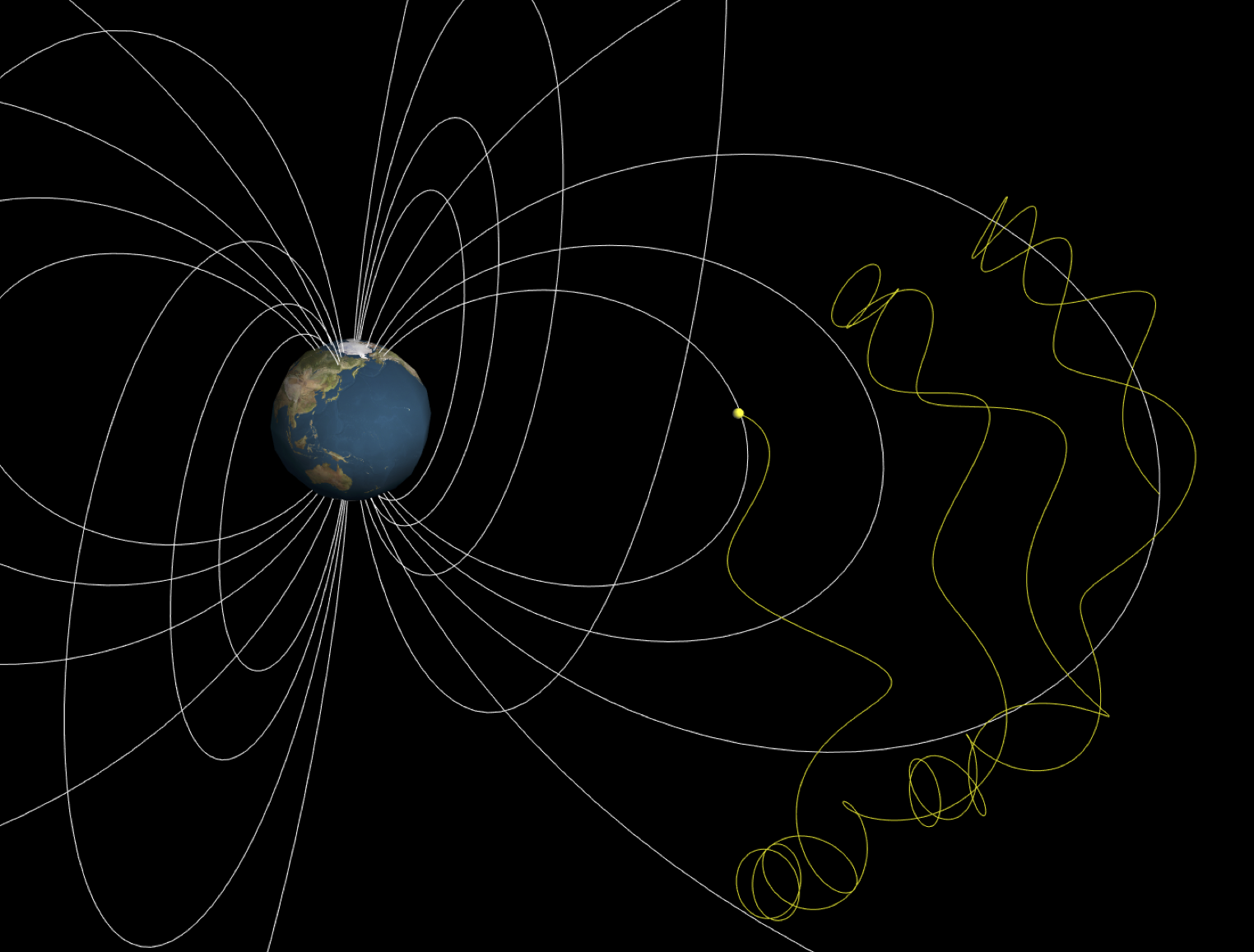
地球磁場を模した系の中での荷電粒子の軌道を計算した例.ちなみに,これはJavaScriptを使って作成されたソフトで,ウェブブラウザ内で動く.軌道追跡の最中にマウスで角度を変えて観察できる.
疑似アニーリングによるプラズマ定常状態計算に関する研究
磁気流体力学(MHD)モデルによるプラズマの定常状態計算は,核融合プラズマ研究等においては基盤的技術の1つである.プラズマに流れがなく,軸対称トーラス型のプラズマなど2次元の場合は,Grad-Shafranov方程式という楕円型偏微分方程式を解けばよいことが知られており,また高速な数値解法も開発されている.しかし,プラズマが流れている場合(軸対称トーラスプラズマならポロイダル方向の流れの場合)や,3次元的な場合については,十分に研究が進んでいない.
本研究では,理想流体(理想MHDを含む)がHamilton系として記述できることを利用し,疑似シミュレーションによってプラズマの定常状態を計算する新しい手法を開発している.疑似アニーリングとは,物理的な運動方程式を基に「改変」した発展方程式を解き,Casimir不変量と呼ばれる系に内在する不変量を保持したままエネルギーを単調変化させ,エネルギーの極値で与えられる定常状態に至らせる方法である.これまでに中性流体での実例はあったが,本研究でプラズマの場合,特に2次元低ベータ簡約化MHDモデルを用いた実例を示した.
さらに,疑似アニーリングでは,初期値を与えた時点でCasimir不変量の値が決定し,定常状態に至るまでその値は原理上変化しない.そこで,疑似アニーリンに入る前にCasimir不変量を望みの値に調整しておく方法も併せて開発し,実際に機能することを示した.
Y. Chikasue and M. Furukawa, Phys. Plasmas, 22, 022511 (2015),
Y. Chikasue and M. Furukawa, J. Fluid Mech., 775, 443 (2015)など.
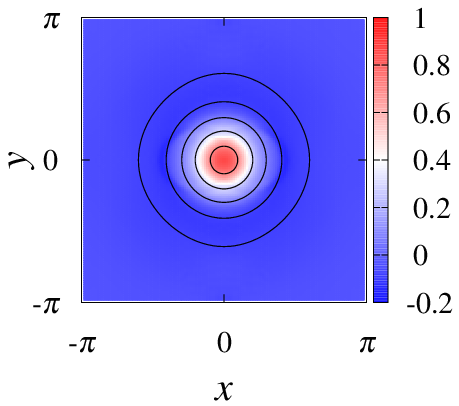
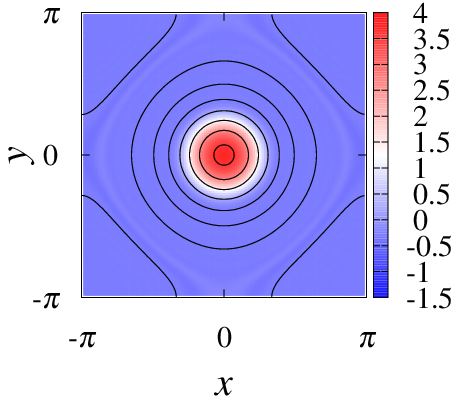
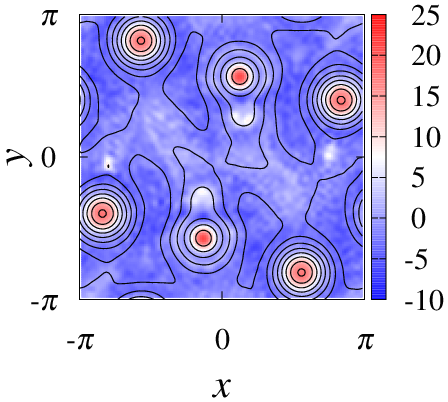
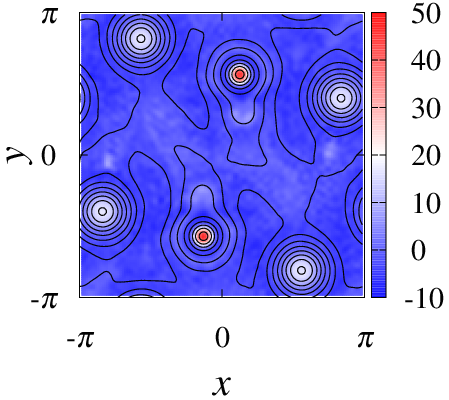
疑似アニーリングによって得られたプラズマ定常状態.上段はCasimir不変量の1つであるクロスヘリシティが小さい場合,下段は大きい場合である.また,左側は等高線が流線でカラーマップは渦度,右側は等高線が磁力線でカラーマップは電流密度を表す.
磁化プラズマにおける境界層(特異摂動)問題の新解法に関する研究
磁化プラズマの巨視的な運動を記述するために,磁気流体力学(MHD)モデルが広く用いられている.核融合を目指した磁場閉じ込めプラズマに関しても,その力学平衡やAlfven波の安定性問題は核融合研究が始まった当初からの中心的研究課題の1つであり,精力的に研究が行われてきた.中でも,Alfven波の波数ベクトルが閉じ込め磁場と垂直になる場所(共鳴面)は,磁力線の張力が働かなくなることに対応してモデル方程式や解に特異性が現れるため,細心の注意を払った精密な解析が必要となる.核融合プラズマは非常に高温であり,電気抵抗はAlfven波の特徴的な時空間スケールで規格化すると(Lundquist数の逆数)10のマイナス12乗にも達する.磁力線張力が効かなくなる共鳴面の付近では,微小効果である電気抵抗や慣性が相対的に重要な働きをするが,その境界層はプラズマサイズに比べて大変薄く,伝統的には漸近接続理論を用いて研究されてきた.この理論は確立されたものであるが,いくつかの本質的困難と,現実的に不可避な数値計算における適用上の困難がある.これらの困難はいずれもMHDモデルの特異性に起因するものであり,超高温プラズマにおいては境界層問題としての扱いが避けられないことから,核融合研究に古くから残る難問である.我々は,この問題に対する新しい接続解法を開発し,実際に数値計算結果も示してその有効性を示した.
M. Furukawa et al., Phys. Plasmas, 17, 052502 (2010),
M. Furukawa et al., Phys. Plasmas, 18, 062502 (2011),
M. Furukawa et al., Phys. Plasmas, 19, 102511 (2012)など.
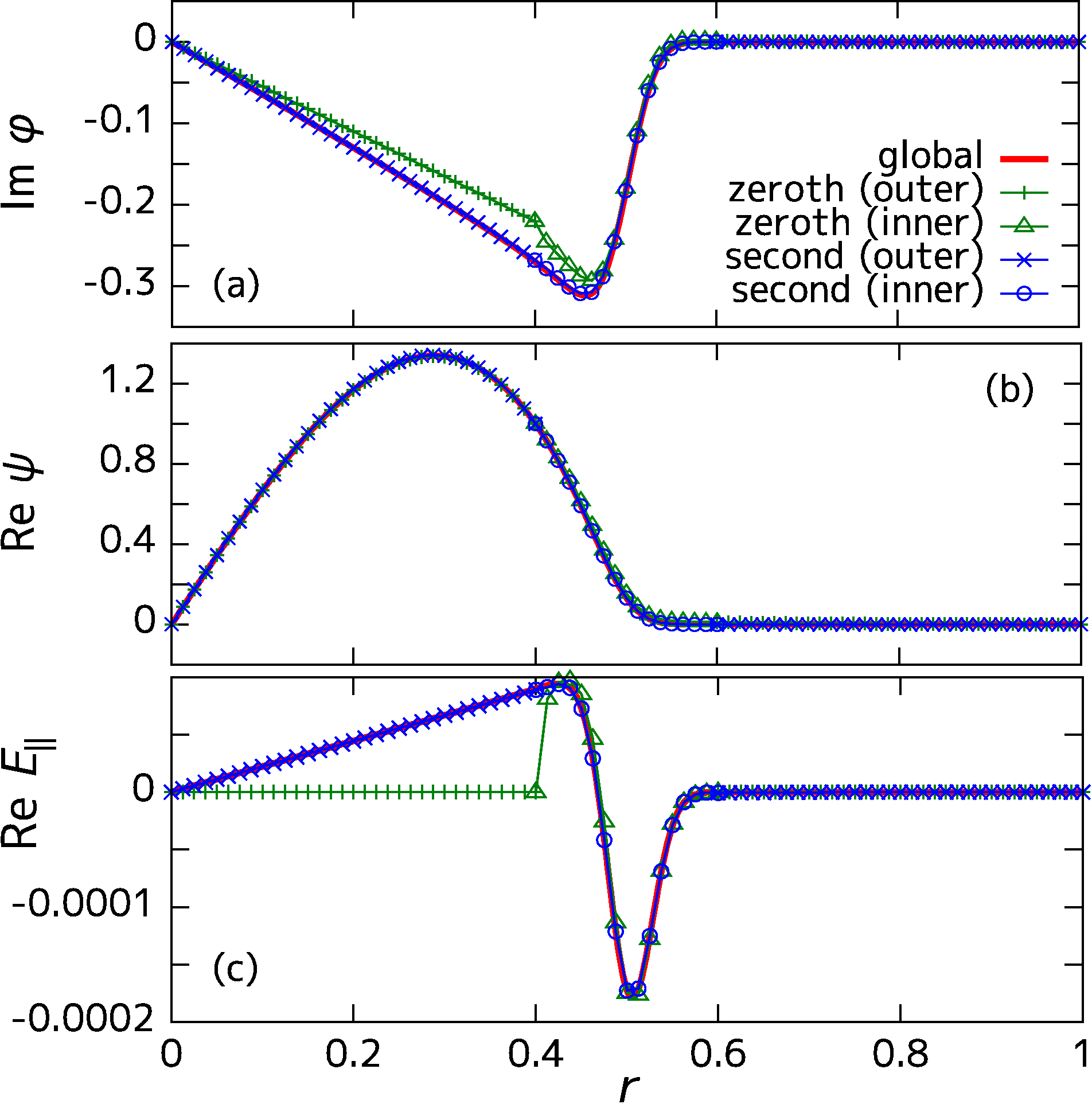
境界層問題に対して新たに開発した接続解法を用い,内部キンクモードの安定性を解析したときのモード構造.2次の摂動まで取り込むことで,これまで慣性なしの理想MHDモデルで扱われてきた領域に電気抵抗と慣性の効果を取り込むことに成功した.
トカマクプラズマへの不整磁場浸透とプラズマ回転による遮蔽に関する研究
近年のトカマク実験では,装置の構造物等に起因する小さな非軸対称磁場(不整磁場)が,Alfven波を介してプラズマ中で増幅され得ることが深刻な問題となっている.この増幅された磁場は,閉じ込めに有害な影響を与える磁気島を生成したり,閉じ込め改善に有効と考えられているプラズマ回転を減速させたりする.これらは,トカマクの閉じ込めを劣化させ,しばしばディスラプションを引き起こす原因となる新古典テアリングモード(neoclassical tearing mode, NTM)や抵抗性壁モード(resistive wall mode, RWM)に密接に関係している.したがって,不整磁場がプラズマ中に浸透し増幅されるメカニズムとその様子を物理的に理解し,さらには不整磁場の浸透を抑える方法を確立することは,核融合開発において重要なテーマとなっている.我々は,簡約化MHDモデルの数値シミュレーションにより,特にプラズマ回転による不整磁場の遮蔽について研究した.プラズマ回転は,Alfven波の周波数をDopplerシフトさせる.このため,磁気島を生成させる原因となる電気抵抗が働く場所(Alfven共鳴面)が2枚の面にスプリットし,不整磁場の空間的構造と閉じ込め磁場のねじれピッチが共鳴する場所(有理面)からずれる.Alfven共鳴面と有理面の間の距離が,電気抵抗によって決まる抵抗層の幅よりも広くなると,十分な遮蔽効果が得られることを明らかにした.
M. Furukawa et al., Nucl. Fusion, 49, 075018 (2009)など.
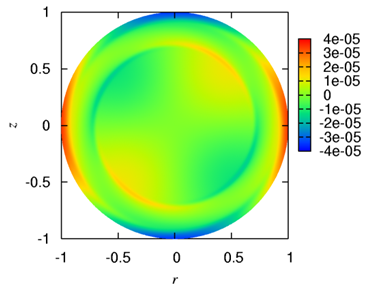
外的に与えた不整磁場がプラズマ中に浸透する様子を簡約化MHDモデルを用いて数値シミュレーションした.プラズマ回転により,Alfven共鳴面が2枚にスプリットし有理面からずれるため,不整磁場のプラズマ中への浸透や磁気島の生成が抑えられる.
シア回転するトーラスプラズマにおけるバルーニングモード安定性に関する研究
磁化プラズマのAlfven波安定性は,磁場閉じ込め核融合プラズマを安定に長時間保持できるかどうかに直結し,精力的に研究が行われてきた.特に,閉じ込め領域の中心と端との間の大きな圧力勾配が駆動する不安定性は,閉じ込め磁場を横切る方向には短波長,磁場に沿った方向には長波長な空間構造をもち,WKB法を用いた簡約化モデルにより解析が行われてきた.これらのAlfven波安定性の問題は,力学平衡状態でプラズマ流がなければエルミート演算子で記述され,そのスペクトル理論は確立されている.しかし,平衡プラズマ流がある場合には,非エルミート演算子で記述され,数学的な理論は確立されていない.近年,磁化プラズマの閉じ込め実験において,プラズマ流が重要な役割を担っていることが多数報告されるようになり,数理的な意義だけではなく,現実的にも重要な問題として改めて注目が集まっている.我々は,流れをもつプラズマのAlfven波安定性に関して,時間依存するアイコナールを用いて短波長近似したモデル方程式(時間依存する係数をもつ1次元連立波動方程式)を数値シミュレーションし,流れシアが圧力勾配駆動の不安定性を安定化するメカニズムを発見した.このメカニズムの研究では,Alfven波の連続スペクトルを点スペクトルで"上手く"近似する正規直交基底を構成するための方法を開発し,時間とともに変化していく正規直交基底系で数値シミュレーション結果を展開することによって,不安定モードから安定モードへとエネルギーが移送されていく様子を捉えることに成功した.
また,この方法を磁気圏型プラズマ閉じ込めに適用したシミュレーションも行い,プラズマのシア流によってバルーニングモードが時間漸近的には安定化されること,しかしトカマクプラズマとは安定化の様子が若干異なることも明らかにした.
M. Furukawa et al., Phys. Rev. Lett., 94, 175001 (2005)など.
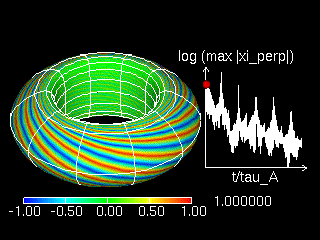
トカマクプラズマにおけるバルーニングモード安定性解析に,トロイダル方向へのシア回転効果を含めたシミュレーション結果.バルーニングモードの振幅は,時間とともに減少していく(シア回転による安定化).
トロイダル回転・非等方圧力をもつトーラスプラズマの力学的平衡に関する研究
磁気圏型の磁場配位によるプラズマ閉じ込めの性質,特にプラズマのMHD平衡に対するトロイダル回転や非等方圧力の効果について調べるため,MHD平衡の数値計算コードを開発した.軸対称トーラスプラズマのMHD平衡は,Grad-Shafranov方程式と呼ばれる楕円型2階偏微分方程式で記述される.本研究で解いているのは,そのトロイダル回転・圧力非等方性を含めた拡張版である.静電場を求めるときに解くPoisson方程式と同じタイプの方程式であり,よく知られている高速数値解法を本コードでも用いている.
プラズマの回転や圧力非等方性がなければ,MHD平衡では磁力線に沿って圧力が一定となる.しかし,それらがある場合は磁力線に沿って圧力が変化し得る.圧力に非等方性がある場合,磁力線方向の力のバランス式も解く必要があり,磁力線上での圧力変化の様子は圧力の非等方性によって異なる.磁力線方向の圧力(p_parallel)が磁力線を横切る方向の圧力(p_perp)よりも大きければ,磁場が強い領域で圧力が高くなり,逆に p_perp が p_parallel よりも大きければ,磁場が弱い領域で圧力が高くなる.ベータ値は圧力を磁気圧で規格化した量なので,磁場が強い領域で圧力が高くなる p_perp < p_parallel のケースでは,閉じ込め領域全体に比較的高いベータ値が実現するが,逆に磁場が弱い領域で圧力が高くなる p_perp > p_parallel のケースでは,局所的にベータが高い場所が現れるが,閉じ込め領域全体としては低ベータに止まる傾向がある.
なお,このコードを応用して,非中性(純電子)プラズマの平衡状態も計算することができる.
M. Furukawa, Phys. Plasmas, 21, 012511 (2014)など.
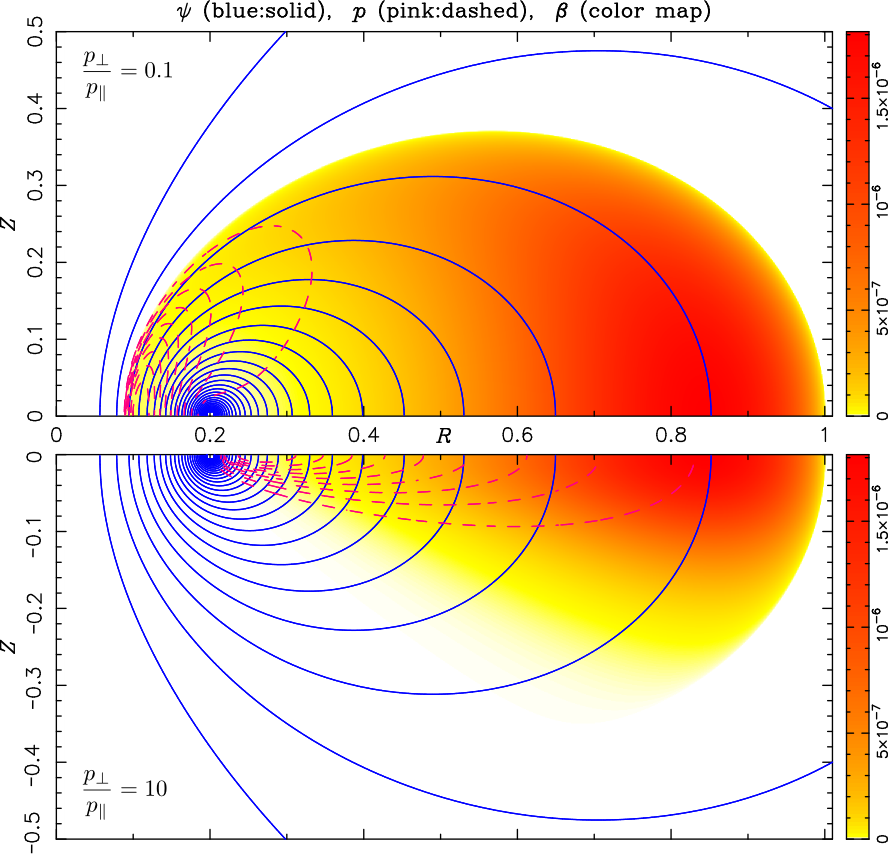
磁気圏型の磁場配位によるプラズマ閉じ込めに対する非等方圧力効果を調べるために,シンプルなリング電流により磁気圏を模擬した磁場配位を作り,その磁場によるプラズマ閉じ込めのMHD平衡を計算した.磁気圏型磁場配位では高ベータプラズマの閉じ込めが可能であることが実験的にも示されているが,この図では,非線形性によって磁場配位がリング電流のものから変化しない程度のベータ値で,圧力非等方性がMHD平衡にどのような効果をもつかを示している.上半面にはp_perp / p_parallel = 0.1,下半面にはp_perp / p_parallel = 10の場合の平衡の,磁束関数の等高線(青の実線),圧力の等高線(ピンクの破線),ベータ値(カラーマップ)を示している.
降着円盤における磁気回転不安定性に関する研究
磁化プラズマは,宇宙にも広く存在する.降着円盤においては,観測されるプラズマの中心天体への降着率を説明するために,プラズマ回転と磁場が相互作用して起こる磁気回転不安定性が注目されている.本研究では,MHDモデルを用い,円盤中心の特異性が磁気回転不安定性に与える効果について調べた.Kepler回転を仮定すると,円盤中心はAlfven波の方程式において不確定特異点となる.このことに起因し,波の周波数は,非可算無限個の点スペクトル(固有値)の連続帯となる.それぞれの点スペクトルに対応する固有関数は,自乗可積分である.
磁化プラズマ中のAlfven波に関して,不安定性を示す点スペクトルが得られることはしばしばあるが,通常は連続帯にはなっていない.そのため,ある初期値からスタートして時間発展を追うと,波の空間構造は,最も成長率(波の周波数の虚部)の大きい固有値に対応する固有関数に程なく一致する.しかし,本研究で得られた結果では,最も成長率の大きい固有値の無限近くに2番目の固有値があり…,という状況になっている.したがって,ある初期値からスタートして時間発展を追ったときに,波の空間構造が成長率の最も大きい固有関数に一致するまでには無限の時間が掛かり,シミュレーションを行う間では波の空間構造は変化し続ける.
M. Furukawa et al., Astrophys. J., 659, 1496 (2009)など.
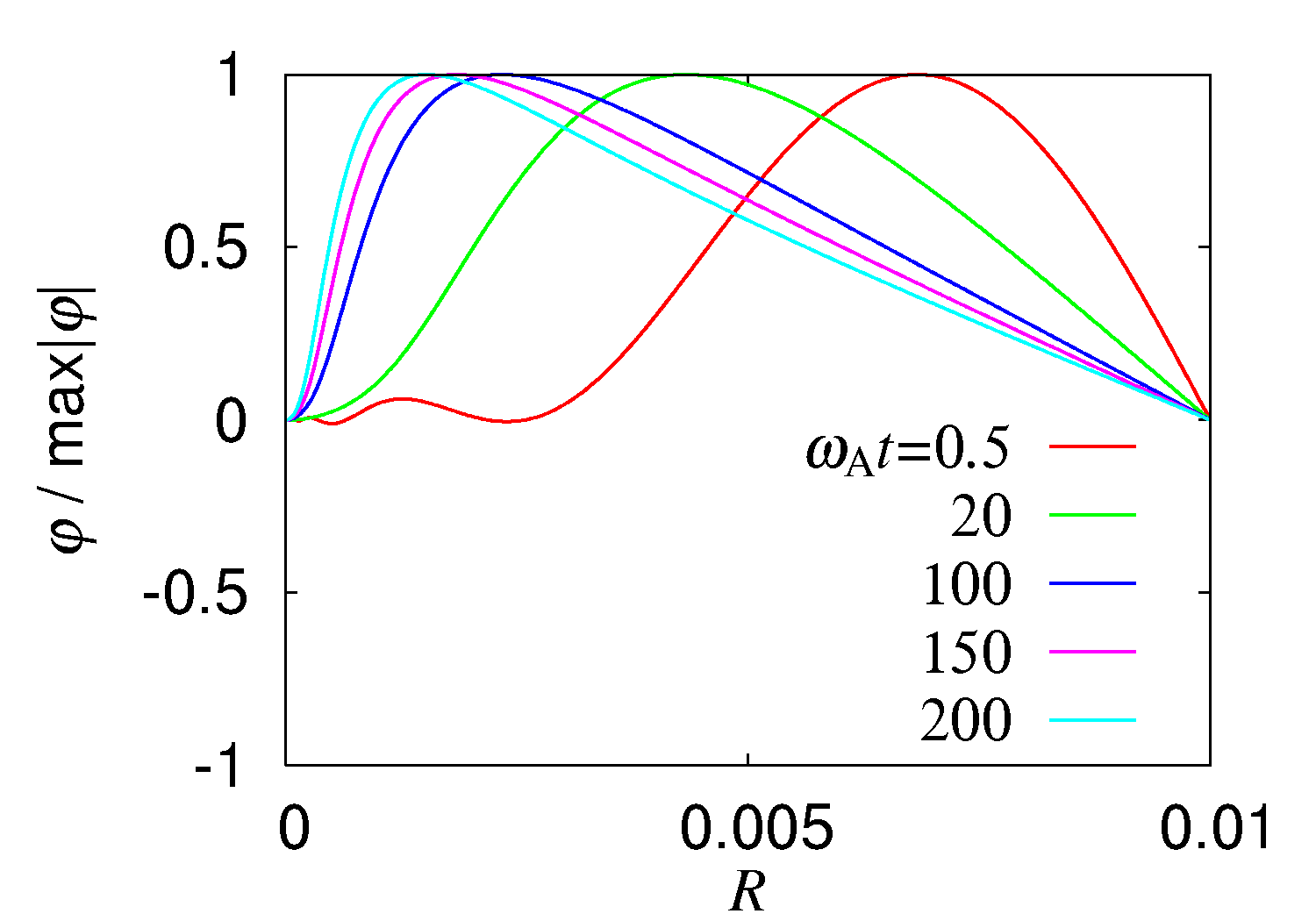
降着円盤中心の特異点に起因する固有値の連続帯のため,磁気回転不安定性の空間構造が時間とともに変化していく様子が観察できる.