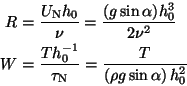We discuss free-surface flow motion of viscous liquid
falling down a solid wall,
referred to as falling film flows.
If we take the ![]() -axis downward along the wall
and the
-axis downward along the wall
and the ![]() -axis perpendicular to it,
denoting the velocity field
by
-axis perpendicular to it,
denoting the velocity field
by
![]() and the surface location by
and the surface location by ![]() ,
then the basic equations are written as follows:
,
then the basic equations are written as follows:
It is the convention to introduce the representative film thickness ![]() and thereby define two non-dimensional parameters
(besides the inclination angle
and thereby define two non-dimensional parameters
(besides the inclination angle ![]() ), namely
), namely