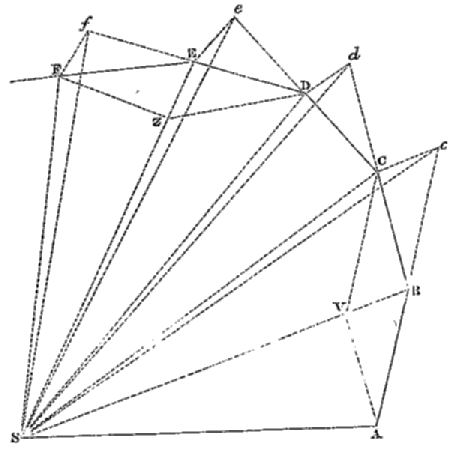
ひとまず時間をΔtごとに区切って考えよう。 最初の時刻に惑星がAにあり、 その次の時刻(Δtだけ時間が経過したあと)にはBに来ているとする。 もし惑星が力を受けていないなら、 第1法則により、惑星は等速直線運動をおこない、cに来るはずである。 しかしこの軌道は、太陽Sからの引力によって曲げられ、 惑星はcの代わりにCに来ることになる。 太陽からの引力は直線BS方向にはたらくから、軌道の変化をあらわすcCは、 BSに平行である(図ではこのことは平行四辺形BVCcで示されている)。 したがって三角形SABと三角形SBCは底辺SBが共通で高さが等しく、 ゆえに両者の面積は等しい。 それ以降の時刻についても同様である。 したがって、 太陽と惑星とを結ぶ直線が、 時刻 t = t0 から t = tn までに通過する面積は、 経過時間 tn - t0 に比例する。
ここではΔtを有限にして考えたために軌道が折れ線状になっているが、 軌道が曲線となる場合を考えるには、Δt → 0 の極限をとればよい。