g(x) =
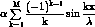
のグラフを描いてみよ(α,λは定数)。
上の問題で f=g とした場合の解(あるいは 少なくとも長時間経過後の解)は理論的に求められるはずである。 こうして求められた解と、上の数値計算の結果を比較してみよ。
1997-07-08 大西・大信田
3階の定数係数の常微分方程式
A y''' + B y'' + C y' + D y = f(x); A≠0
を考える。 (y' = dy/dx etc.)
まず f(x) = 0 のときを考える。 解を求めるにはどうしたらいいか? 具体例として (A,B,C,D) = (1,-3,-1,3) の場合や (A,B,C,D) = (1,-3,3,1) の場合を考えよ。
さらに f がゼロでないときは 定数変化法のような手法を用いなくてはならない。 一般的にどのようにしたらいいか考えよ。 また何か具体例を考えて解いてみよ。
線形・定数係数の常微分方程式である。 これを解くには 2階の場合の方法をすなおに拡張すれば良い。
まずf=0の場合、y=[const.]×exp{λ*x}のような解をさがす。
代入すると
A*λ^3 + B*λ^2 + C*λ + D = 0 … (★)
のような3次方程式(特性方程式)が得られる。
この方程式が異なる3つの根 λ1,λ2,λ3 をもつなら、
一次独立な解(exp{λj*x}; j=1,2,3)が3つ得られたことになり、
一般解は 定数p,q,rを用いて
y = p*exp{λ1*x} + q*exp{λ2*x} + r*exp{λ3*x}
のようになる。
(なおλが複素根であっても
p,q,rを適当に選んでyを実数にすることができる。)
もし特性方程式(★)が重根をもつなら、
上の方法では一次独立な解は1つまたは2つしか得られない。
この場合については下の具体例を参照されたい。
具体例 (f=0とする):
つまり y''' - 3 y'' - y' + 3y = 0 という方程式。
特性方程式の解は λ=-1,1,3 であり、
ただちに一般解
y = p*e^{-x} + q*e^{x} + r*e^{3*x} ; p,q,rは定数
が得られる。
(A,B,C,D) = (1,-3,3,1) の場合
[これは実は出題ミスで 本当は(1,-3,3,-1)のつもりだったのだが、
とにかくこのまま解いてみる。]
特性方程式は
λ^3 - 3*λ^2 + 3*λ + 1 = 0
つまり
(λ-1)^3 = -2
となり、
解は数値的に
λ = -0.26, 1.63±1.09*i
である。
これを求めるには
2^{1/3} を数値的に計算し 1の3乗根と組み合わせてもいいし、
また実数の根をNewton法で求め、
そのあと組み立て除法を実行しても良い。
したがって一般解は
y = p*e^{-0.26*x} + q*e^{(1.63+1.09*i)*x} + r*e^{(1.63-1.09*i)*x}
であり、
これは q = (α-iβ)/2, r = (α+iβ)/2 と
置くことにより
y = p*e^{-0.26*x} + e^{1.63*x}*(α*cos(1.09*x)+β*sin(1.09*x))
のように実数で書くこともできる。
特性方程式は
λ^3 - 3*λ^2 + 3*λ - 1 = 0
で、
これはλ=1を3重根に持つ。
これだけでは解はひとつ(exp{x})しか得られない。
そこで
y = Y*exp{x}; Yはxの関数
として もとの微分方程式に代入してみると
Y'''=0
となる。
これはp,q,rを任意定数として Y = p + q*x + r*x^2 という解をもち、
したがって もとの方程式の一般解が
y = ( p + q*x + r*x^2 ) * e^{x}
のように得られる。
上のような方法により、f=0 としたときの一般解(同次解)が
y = p*f(x) + q*g(x) + r*h(x) … (※)
のような形で求められたとしよう。 ここで p,q,r は 定数である。
さて f≠0 の場合の一般解を求めるために(※)を用いることは、
少なくとも理論的には可能であるが、このとき
p,q,r は もはや定数ではなく
xの関数であると考えなければならない(定数変化法)。
ただしこれだけでは自由度が多すぎるので、
次のような条件をつけることにしよう。
[どうもこのへんの話は天下り的になってしまうが、
一応『f=0のときp'=q'=r'=0』ということと
つじつまは合っている。]
これらの条件 および(※)を 微分方程式に代入し
整理すると
p' * f'' + q' * g'' + r' * h'' = f(x)/A … (3)
のようになる。
ここで(1),(2),(3)は p',q',r'に関する1次方程式であるから、
これを解いて(p',q',r')を求め、積分すれば良い。
[このとき出てくる行列はWronski行列と呼ばれる。]
もし f が 多項式・三角関数・指数関数などで与えられているなら、
実際には特解の形を予想し
代入して係数を決める方法(未定係数法)のほうが
はるかに楽である。
たとえば y''' - y = 2*x^2 のような微分方程式は
多項式の特解をもつことが容易に推察できる。
一般解は
y = p*e^{x} + e^{-x/2}*( q*cos(γ*x) + r*sin(γ*x) ) - 2*x^2
のように同次解と特解の和になる。
これを係数変化法で求めるのは、不可能ではないが かなり大変である。
微分方程式
(d/dt)^2 y + ω^2 y = f(t)
および初期条件
y_{t=0} = 0, (d/dt)y_{t=0} = 0
によって定められる初期値問題を考える
(とりあえず ω=1 としよう)。
具体的にfが与えられているとして、 yを求める電算機プログラムを作成せよ。
のような場合に y (およびf)のグラフを描け。
(定数γの値をいるいろ変えてみよ。)
解の短時間的なふるまい(t=0の直後)と
長時間的なふるまい(t→∞)を考察せよ。
いま Mを適当に大きな定数として(M=10くらい)、関数
g(x) =
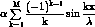
のグラフを描いてみよ(α,λは定数)。
上の問題で f=g とした場合の解(あるいは
少なくとも長時間経過後の解)は理論的に求められるはずである。
こうして求められた解と、上の数値計算の結果を比較してみよ。
調和振動子に外力fを加えた系のシミュレーションである。 減衰は入っていない。
数値計算プログラムの例を作成したので、 ソースコードを見たり、実際に動かしたりしてみるとよい。 ファイル oscil.f + force1.fの組合せが 例(1)の計算、 oscil.f + force2.fが 例(2)の計算プログラムとなる。
例(2)のfは T=1/γを周期とする周期関数で、
しばしば『鋸歯状波』あるいは『三角波』と呼ばれる。
周期関数であるから、単振動の場合の類推で、
外力の周期Tと振動子の固有周期(=2π/ω)とが一致したとき
共振が起きることが予想される。
興味ぶかいのは、Tが固有周期と一致する場合だけでなく
固有周期のn倍と一致するときにも共振が見られることである。
もしfが純粋に正弦波的だったら このようなことは起こらない。
波形が正弦波とは異なっている場合にのみ、
このように n=1だけでなく n=2,3,...でも共振が起こり得る。
級数
g(x) =
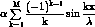
は Mを大きくすると 全体として
周期2πλの三角波に近づく(グラフを見よ)。
このg(x)を外力とした場合の特解は
(未定係数法の考え方からいくと)やはり
sin(kx/λ)に適当な係数をかけたものの和で書けるはずだ。
実際に計算してみると、k/λ=ω となる項がある場合に その係数が
無限大になる。
これは まさにT=2πλが2πωの整数倍に一致する場合に起きることである。
正弦関数 sin x は、 微分方程式 y'' + y = 0 と 初期条件 y(0)=0, y'(0)=1 から 定められる関数であると考えることができる。 このことを利用して、sin x の級数解を求めよ。 求めた級数解の部分和(第1項のみ,第2項まで,第3項まで,...以下同様)を グラフに示し、sin x のグラフと比較せよ。
初期値問題 f' + 2x f = 0 , f(0) = 1 の解を 級数の形で求め、上と同様に部分和を図示せよ。 また厳密解を求めて図示し、比較せよ。 教科書4.2.(p144)を参考にして、結果を考察せよ (ヒント:収束半径は?)。
正弦関数の展開を
sin x = c0 + c1 * x + c2 * x^2 + … + cj * x^{j} + …
のように仮定し、微分方程式に代入すると、
漸化式
c{j} = - c{j-2}/( j*(j-1) )
が得られる。 ここで c0 = 0, c1 = 1 を 考慮すると
sin x = x - (1/3!)*x^3 + (1/5!)*x^5 - (1/7!)*x^7 + …
のようになる。
上の結果は無限級数であるが、
これを有限の項で打ち切った場合のグラフを示す。
(あきらかに奇関数なのでx≧0の部分のみで十分である。)
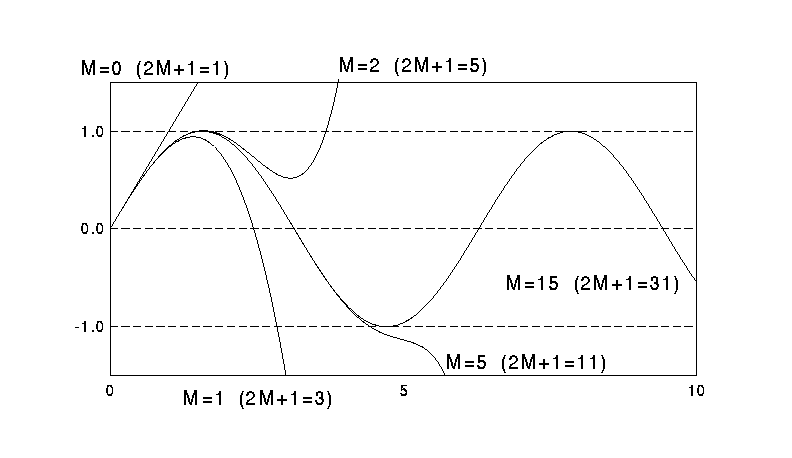
原点(x=0)に近い所ほど早く sin x に収束しているのが分かる。
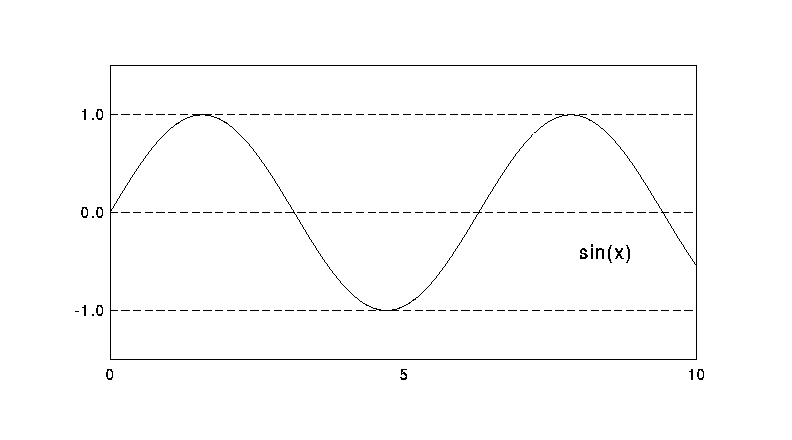
級数の収束半径は無限大だから、xがいくらであろうと
級数の値は 項数→∞ の極限で sin x に収束する。
しかし |x|が大きいほど収束は遅く、
たとえばx=10での値が収束に向かうためには
項数は10以上でなければならない。
やはり収束半径は無限大であるがxが大きいところでの収束が遅い例として
f' + 2*x*f = 0; f(0)=1
の解が挙げられる。
級数解は
f = 1 - x^2 + (1/2!)*x^4 + (1/3!)*x^6 - …
であり、これは項数が無限大のとき
すべてのxの値について
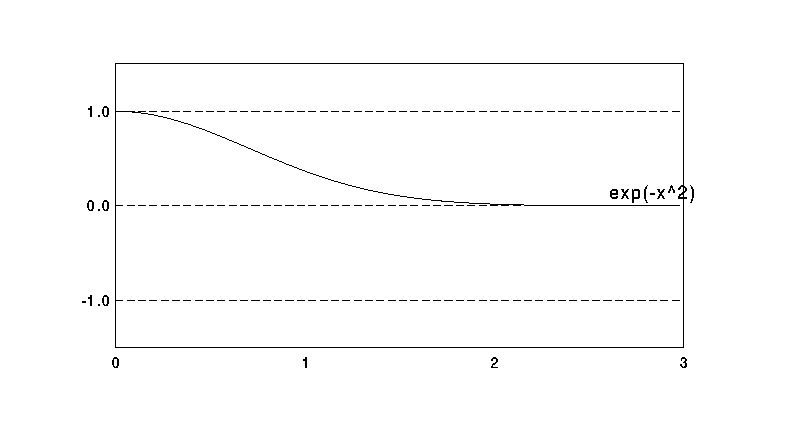
厳密解 f = e^{-x^2} に収束するが、
|x|が大きいところでの収束は遅く、
たとえばx=10で収束を得るためには
項数は100(=10^2)以上なければならない。
実際には級数が収束する前に
計算機の精度のほうが限界に達するであろう。
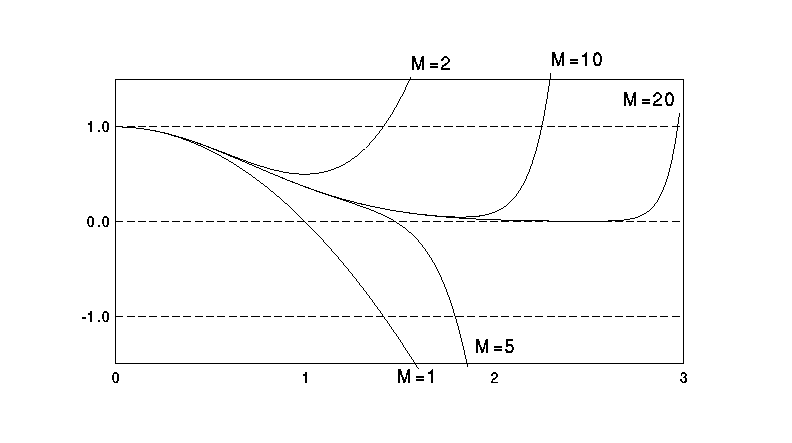
ついでながら後者の例では g=1/fとしてgの展開を計算し
これからfを求めるという手がある。
こうするとわずか2項か3項ですばらしい収束を得ることができる。
しかし残念ながら
この方法は正弦関数には適用できない(ゼロでの割算が生じるため)。
質問、まちがいの指摘などは <ooshida@damp.tottori-u.ac.jp> まで。