[Next: References]
[Up: Regularized long-wave expansion]
[Prev: Failure of Benney's long-wave]
Though the long-wave expansion is expected to converge
for 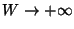 with
with 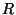 kept finite,
it is quite doubtful
whether it converges for finite
kept finite,
it is quite doubtful
whether it converges for finite 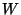 and finite
and finite 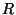 .
The failure shown by Salamon et al.
seems to suggest that
the long-wave expansion is poorly convergent.
.
The failure shown by Salamon et al.
seems to suggest that
the long-wave expansion is poorly convergent.
As a model of the ``poor convergence'',
let us consider a linear PDE
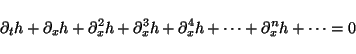 |
(6) |
which contains, formally, an infinite number of terms.
Since 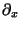 is not a bounded operator,
the left-hand side diverges and therefore it seems meaningless.
However, by letting
is not a bounded operator,
the left-hand side diverges and therefore it seems meaningless.
However, by letting 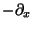 operate upon Eq. (6)
and then adding the result to Eq. (6),
we find a PDE containing only a finite number of terms!
The idea is to regard Benney's long-wave expansion
as Taylor expansion around
operate upon Eq. (6)
and then adding the result to Eq. (6),
we find a PDE containing only a finite number of terms!
The idea is to regard Benney's long-wave expansion
as Taylor expansion around 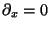 and then replace it by Pade' approximation.
and then replace it by Pade' approximation.
This procedure can be applied to Eq. (4)
which is a nonlinear PDE[6].
In terms of undetermined functions
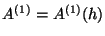 and
and
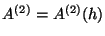 we define
we define
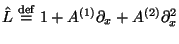 and thereby
and thereby
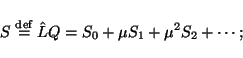 |
(7) |
by remembering
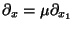 , we have
, we have
and so on.
According to the philosophy of Pade' approximation,
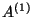 and
and 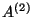 are determined so that ``
are determined so that ``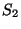 may vanish''
which constitutes
the regularization of the long-wave expansion (4).
The result is
may vanish''
which constitutes
the regularization of the long-wave expansion (4).
The result is
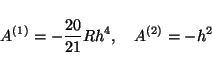 |
(8) |
which leads to the regularized equation
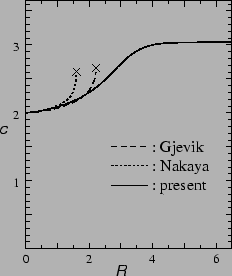
Numerical solutions of Eq. (9)
are compared with those of two long-wave equations (see figure).
The failure is successfully avoided,
at least qualitatively.
It is found
that, for
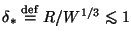 ,
Eq. (9) is quantitatively valid as well.
,
Eq. (9) is quantitatively valid as well.
[Next: References]
[Up: Regularized long-wave expansion]
[Prev: Failure of Benney's long-wave]
[Top]
Author: OOSHIDA Takeshi
ooshida@damp.tottori-u.ac.jp
2000-08-24
![]() with
with ![]() kept finite,
it is quite doubtful
whether it converges for finite
kept finite,
it is quite doubtful
whether it converges for finite ![]() and finite
and finite ![]() .
The failure shown by Salamon et al.
seems to suggest that
the long-wave expansion is poorly convergent.
.
The failure shown by Salamon et al.
seems to suggest that
the long-wave expansion is poorly convergent.
![]() and
and
![]() we define
we define
![]() and thereby
and thereby
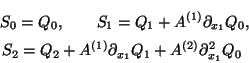
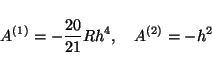
![]() ,
Eq. (9) is quantitatively valid as well.
,
Eq. (9) is quantitatively valid as well.