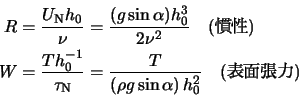[次に進む: 長波展開]
[上に戻る: Regularized long-wave expansion]
[前に戻る: Regularized long-wave expansion]
斜面上を薄い層となって流れる,
自由表面をもつ粘性流体の運動(液膜流)を考察する.
斜面を下る方向に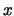 軸, 法線方向に
軸, 法線方向に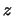 軸をとり,
速度場を
軸をとり,
速度場を
![$\mathbf{u}= {}^t\left[\, u(x,z,t),\, w(x,z,t) \, \right]$](jp_img3.gif) ,
自由表面の位置を
,
自由表面の位置を 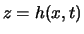 とすると,
基礎方程式系は以下のように書ける:
とすると,
基礎方程式系は以下のように書ける:
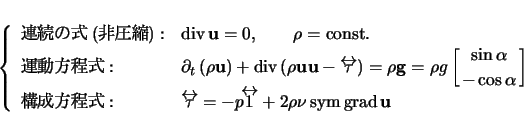 |
(1) |
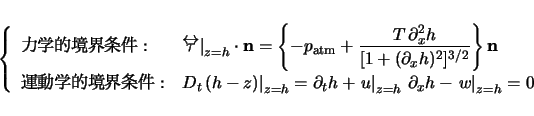 |
(2) |
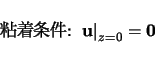 |
(3) |
慣習に従い, 液膜の代表的な厚さ 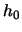 を導入し,
無次元パラメータとして
を導入し,
無次元パラメータとして
および斜面の傾斜角 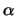 をとる.
常温の水を垂直壁に流す場合,
をとる.
常温の水を垂直壁に流す場合,
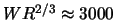 である.
である.
著者: 大信田 丈志
ooshida@damp.tottori-u.ac.jp
2000-08-24
![]() 軸, 法線方向に
軸, 法線方向に![]() 軸をとり,
速度場を
軸をとり,
速度場を
![]() ,
自由表面の位置を
,
自由表面の位置を ![]() とすると,
基礎方程式系は以下のように書ける:
とすると,
基礎方程式系は以下のように書ける:
![]() を導入し,
無次元パラメータとして
を導入し,
無次元パラメータとして