[次に進む: 長波展開の破綻]
[上に戻る: Regularized long-wave expansion]
[前に戻る: 基礎方程式系]
Benney [1]に従って
長波パラメータ 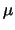 を
を
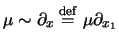 により導入し,
基礎方程式系(1)-(3)を
により導入し,
基礎方程式系(1)-(3)を 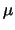 で展開する.
たいていの液体は表面張力が大きいので,
実際に
で展開する.
たいていの液体は表面張力が大きいので,
実際に
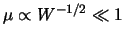 が成り立つことが多い.
こうして速度場
が成り立つことが多い.
こうして速度場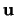 が消去され,
が消去され,
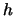 のみを変数とする発展方程式が
のみを変数とする発展方程式が
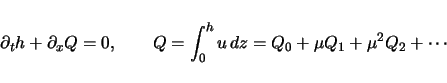 |
(4) |
の形で得られる[2,3,4].
たとえば, 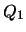 までの結果(Gjevik[2]の長波方程式)は
次のとおり:
までの結果(Gjevik[2]の長波方程式)は
次のとおり:
![\begin{displaymath}
\partial_t h + \frac{2}{3} \partial_x \left[
h^3
+ \left(...
...pha \right) \partial_x h
+ W h^3 \partial_x ^3 h
\right] = 0
\end{displaymath}](jp_img19.gif) |
(5) |
著者: 大信田 丈志
ooshida@damp.tottori-u.ac.jp
2000-08-24
![]() を
を
![]() により導入し,
基礎方程式系(1)-(3)を
により導入し,
基礎方程式系(1)-(3)を ![]() で展開する.
たいていの液体は表面張力が大きいので,
実際に
で展開する.
たいていの液体は表面張力が大きいので,
実際に
![]() が成り立つことが多い.
こうして速度場
が成り立つことが多い.
こうして速度場![]() が消去され,
が消去され,
![]() のみを変数とする発展方程式が
のみを変数とする発展方程式が