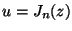
![[J0 と J1 のグラフ]](j0.png)
- 母関数表示:
![\exp[ (z/2) (t-(1/t)) ] = \sum_n^{} J_n(z) t^n](gen4bessel.png)
- 原点の近くで
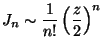
- 遠方(
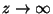 )で
)で
![J_n 〜 \sqrt{((2)/({π}z))} \cos[ z - (π/2)(n+(1/2)) ]](Jn-inf-asympt.png)
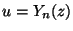
![[Y0 と Y1 のグラフ]](y0.png)
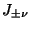 の1次結合として定義:
の1次結合として定義:
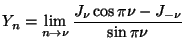
- 原点の近くで
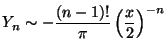 (
(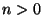 )
)
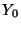 は
原点の近くで対数的に発散
は
原点の近くで対数的に発散
- 遠方(
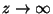 )で
)で
![Y_n 〜 \sqrt{((2)/({π}z))} \sin[ z - (π/2)(n+(1/2)) ]](Yn-inf-asympt.png)
HTML版: 2001-05-02 / PostScript版 (0.75MB)
この文書には、もしかしたら間違いがあるかもしれません。 間違いを発見された場合は、 ooshida@damp.tottori-u.ac.jp まで お知らせいただけると たいへんありがたいです。
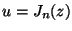
![[J0 と J1 のグラフ]](j0.png)
![\exp[ (z/2) (t-(1/t)) ] = \sum_n^{} J_n(z) t^n](gen4bessel.png)
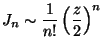
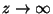 )で
)で
![J_n 〜 \sqrt{((2)/({π}z))} \cos[ z - (π/2)(n+(1/2)) ]](Jn-inf-asympt.png)
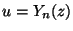
![[Y0 と Y1 のグラフ]](y0.png)
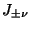 の1次結合として定義:
の1次結合として定義:
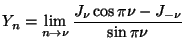
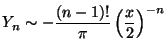 (
(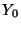 は
原点の近くで対数的に発散
は
原点の近くで対数的に発散
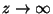 )で
)で
![Y_n 〜 \sqrt{((2)/({π}z))} \sin[ z - (π/2)(n+(1/2)) ]](Yn-inf-asympt.png)
これらはBesselの微分方程式
![[ (1/z)∂_z z∂_z + 1 - ((n^2)/(z^2)) ] u = 0](Eq-Bessel.png)
第2種のBessel関数をNeumann関数と称し、
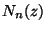 のように書くことも多い。
また
のように書くことも多い。
また
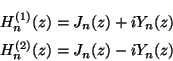
三角関数が指数関数と結びついているように、
Bessel関数は、
変形されたBesselの微分方程式
![[ (1/z)∂_z z∂_z - ( 1 + ((n^2)/(z^2)) ) ] u = 0](M-Eq-Bessel.png)
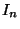 は
は
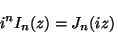
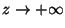 で指数関数的に増大する。
他方、第2種の変形Bessel関数
で指数関数的に増大する。
他方、第2種の変形Bessel関数 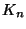 は
原点で対数的またはベキ的に発散し、
は
原点で対数的またはベキ的に発散し、
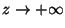 で指数関数的にゼロになるような関数である。
で指数関数的にゼロになるような関数である。
[特殊関数のページに戻る] [物理の部屋に戻る] [ホームページに戻る]