たくさんある。
特に力学では運動方程式はODEだから、ODEを解くことが非常に重要になる。
また、4/20の講義の最後に配ったプリントにあるとおり、
PDE(偏微分方程式)まで含めると、物理のほぼあらゆる分野に
微分方程式(ODEまたはPDE)が登場する。
PDEの解法の定番は「ODEに直して解く」というものなので、
結局、物理のほぼあらゆる分野でODEの知識が必要となることが分かる。
まず、ODEとは「未知の関数の微分を含む等式」だということは しっかり理解できていますか? 赤い教科書のp.5にあるLotka-Volterra方程式の例では、 求めるべき未知関数は (y1(t), y2(t)) で、 この関数は従属変数を2つ含んでいます。 それで、この例は2変数のODEということになるわけです。
微分方程式とは未知の関数の導関数を含む方程式のことだった。 微分方程式には、 常微分方程式(ODE)と偏微分方程式(PDE)がある。 ODEとPDEの違いは何かというと、 未知関数における独立変数の個数の違いである。 ODEの未知関数は x(t) とか (p(s),q(s)) のように 独立変数が1個なのだが、 PDEでは未知関数が u(x,t) のように 2個以上の独立変数を含むものになる。 これにより、PDEは∂u/∂xなどの偏導関数(偏微分)を含むことになる。 他方、ODEには dx/dt のような「通常の」微分が現れる。 だから常微分方程式と言うのである。
大気の運動をあらわす流体力学の方程式を基本として、 エネルギーや水蒸気などの収支釣合を含めたPDEを立て、 その数値解を求める。
良い質問です。 ODEの重要な属性のひとつに「線形同次か、線形非同次か、 どちらでもない(非線形)か」というのがあります。 これを見きわめることが適切な解法を選択するうえで重要です。 詳しくは後日あらためて説明しましょう。
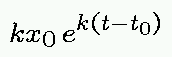 と k x は
違うように見えるのですが?
と k x は
違うように見えるのですが?
dx/dt = k x の解が
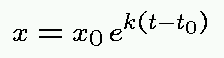 であることを
確認するには、次のようにします:
であることを
確認するには、次のようにします:
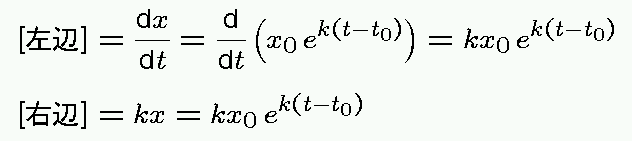
つまり、
k x に 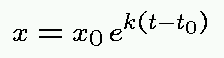 を代入すれば
を代入すれば
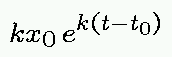 と同じになります。
と同じになります。
見当外れではありません。
今の場合、これも正しい解法です(いわゆる変数分離法)。
ただし、この方法は、理解せずに丸暗記すると
間違った使い方をしてしまう危険性があるため、
あえて説明をあとまわしにしました。
たとえば(4/20の講義で説明したように)、
d2x/dt2 = α2x
のような2階のODEを変数分離法で解こうとしても、
意味不明の式になってしまいます。
(どうやって解いたら良いかについては後日あらためて説明します。)
なお、変数分離法の公式は、
差分の考え方で証明することができます。
たとえば
小谷岳生「ゼロから学ぶ物理数学」 p.22 を見てください。
だいたい次の3つの解き方があると考えてください:
- 差分によって数列に持ち込む
- 変数分離などを用いて積分に持ち込む
- 解の形を推測し、何か適当に置いて代入する
ひとことで答えるなら「場合による」というのが答えです。
解析解が求まる場合は、
最終的な解法としては数列はあまり使いません。
ただし、この講義では、
解法を理解したり証明したりするための手段として
数列を駆使します。
他方、解析解が求まらない場合は、数値解を求めるしかないわけで、
こういう場合には数列の漸化式の考え方が中心になります。
力学とかプロジェクトとか卒業研究とかで
数値解を求める必要が生じる場面は数多くあるので、
その意味では、数列を使う必要は多々あることになると思われます。