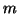 の質点が、
バネからの力 -kx と、
速度に比例する抵抗力
の質点が、
バネからの力 -kx と、
速度に比例する抵抗力 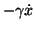 を受けて運動しているとしよう。
この場合、質点の運動方程式は
を受けて運動しているとしよう。
この場合、質点の運動方程式は
2000-11-01
注意! 演習室のプリンタの用紙やトナーには限りがあります。 必要以上にたくさん印刷することは避けてください。 特に、WWWの文書(この文書を含む)は、 なるべくオンラインで見るようにしてもらえると助かります。
質量 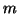 の質点が、
バネからの力 -kx と、
速度に比例する抵抗力
の質点が、
バネからの力 -kx と、
速度に比例する抵抗力 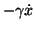 を受けて運動しているとしよう。
この場合、質点の運動方程式は
を受けて運動しているとしよう。
この場合、質点の運動方程式は
※ 無次元化: 式のなかに現われる変数を すべて「次元なし」にするような変数変換のこと。
減衰がない場合、単振動の方程式
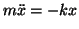 は
は
※ 今の例では位相空間は2次元であるが、一般にそうとは限らない。 たとえば、3次元における質点の運動を表現する場合は6次元空間となる。
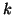 と
と
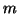 を組み合わせて
時間の次元をもつ基準量
を組み合わせて
時間の次元をもつ基準量
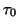 を作り、
を作り、
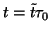 と置く。
と置く。
![(d/dt)[p,q] = ...](Num0011img12.gif) の形に書き直し、
この方程式を解く数値計算プログラムを作成せよ。
の形に書き直し、
この方程式を解く数値計算プログラムを作成せよ。
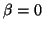 の場合(減衰がない場合)を考える。
いくつかの適当に決めた初期条件に対して、
位相空間における (p, q)の軌跡を
数値計算で求めて図示し、明日(11月2日)の夕方までに提出せよ。
の場合(減衰がない場合)を考える。
いくつかの適当に決めた初期条件に対して、
位相空間における (p, q)の軌跡を
数値計算で求めて図示し、明日(11月2日)の夕方までに提出せよ。
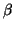 =0.5,
1.5, 2.5 の場合の数値解を求め、
=0.5,
1.5, 2.5 の場合の数値解を求め、
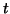 の関数として図示せよ。
なお、初期条件は10月の課題[1]と同じとする。
の関数として図示せよ。
なお、初期条件は10月の課題[1]と同じとする。
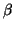 の値に対して、
さまざまな初期条件に対する減衰振動の運動を計算し、
その結果を、
位相空間における (p, q)の軌跡として図示せよ。
たとえば
の値に対して、
さまざまな初期条件に対する減衰振動の運動を計算し、
その結果を、
位相空間における (p, q)の軌跡として図示せよ。
たとえば 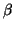 =0.1 から
=0.1 から
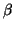 =3.5 くらいまで
10とおりほどの
=3.5 くらいまで
10とおりほどの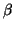 の値について計算し、
その結果のなかから代表的なものを選んで考察せよ(計算結果を
すべて提出する必要はない)。
の値について計算し、
その結果のなかから代表的なものを選んで考察せよ(計算結果を
すべて提出する必要はない)。
これらの課題をレポートにまとめ、 11月27日の朝までに 事務室前のレポート箱に提出すること。