長波展開は ![]() を有限に保って
を有限に保って ![]() とすれば
収束するはずだが,
有限の
とすれば
収束するはずだが,
有限の![]() と有限の
と有限の![]() に対して収束するかどうかは疑わしい.
Salamonらが示した長波展開の破綻は,
長波展開の収束性に問題があることを示しているように思われる.
に対して収束するかどうかは疑わしい.
Salamonらが示した長波展開の破綻は,
長波展開の収束性に問題があることを示しているように思われる.
収束性が悪い場合のモデルとして,
形式的に, 無限個の項をもつ線形の微分方程式
この手続きを, 非線形方程式(4)に拡張する[6].
未定の関数
![]() および
および
![]() を用いて
演算子
を用いて
演算子
![]() を定義し,
を定義し,
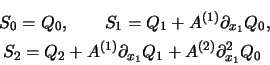
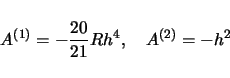 |
(8) |
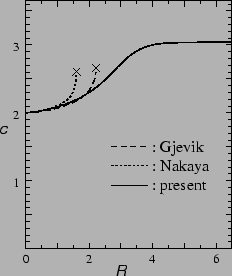
方程式(9)の数値解を求め,
長波展開の結果と比較したのが右上の図である.
長波展開の破綻は, 少なくとも定性的には回避されている.
また,
![]() の範囲では,
方程式(9)は定量的にも正しい結果を再現する.
の範囲では,
方程式(9)は定量的にも正しい結果を再現する.