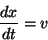 |
(1) |
2000-11-17 更新 / 2008-06-22 微更新
もし「○○をルンゲクッタで解け」とかいう宿題を出されていて、 その答えを探してここに来たのなら、以下の内容を読む前に、 宿題を出した先生の意図は何であるかを ちょっと考えてみてください。 もしかすると、先生が本当に求めているのは、 数値計算結果をレポートとして提出することではなく、 あなたが数値計算プログラムを自力で書けるようになること なのではないでしょうか?
そのへんをよくわきまえた上で、先生の意図に応えられるような形で 以下の内容を参考にされたら良いと思います。
参考: 「教えて! goo」に宿題を頼む前に考えてほしいこと
常微分方程式の数値解法でまず始めに習うのが Euler法である。 ただし、Euler法をそのまま用いるのは実用的でなく、 実際には より洗練された形を用いることが多い。 ここでは、改良Euler法(中点法)と、 その発展形であるRunge-Kutta法について説明する。
常微分方程式
![(x[j+1] - x[j])/dt = v[j]](discrete.gif)
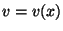 または
または 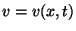 であり、また
であり、また
![x[j]](xj.gif) は
時刻
は
時刻 ![t = t[j] = t[0] + j dt](tj=.gif) における
における
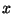 の値を示す。
分母を払って
の値を示す。
分母を払って
例として、
運動方程式 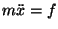 を
を
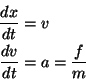
反復 {
a[j] = (x[j]に対応する加速度)
x[j+1] = x[j] + v[j]*dt
v[j+1] = v[j] + a[j]*dt
}
のような感じになる。
※ 本当は配列を使わずに書けるが、 ここでは分かりやすいように配列を用いている。
実際にEuler法で数値計算をしてみると、 そのままでは誤差が大きくて使いものにならない場合が多い。 たとえば、惑星の軌道が楕円軌道になるはずの場合でも、 もとの位置に戻ってこないで少しずれたりする。 もちろん dtをものすごく小さくすれば良いのだが、 こんどはステップ数が多くなって大変である。
そこで、次のように改良してみる:
反復 {
a[j] = (x[j]に対応する加速度)
xh = x[j] + v[j]*(dt/2)
vh = v[j] + a[j]*(dt/2)
ah = (xhに対応する加速度)
x[j+1] = x[j] + vh*dt
v[j+1] = v[j] + ah*dt
}
つまり、Euler法の右辺を
![x[j]](xj.gif) とする代わりに、
いわば
とする代わりに、
いわば
![x[j+1/2]](x_half.gif) のように
半ステップだけ進めた値を用いるのである(具体的なことは
常微分方程式のプログラム例を
参考にしてほしい)。
この方法は「改良Euler法」
あるいは「中点法」「Heunの矩形公式」などと呼ばれ、
Euler法に比べるとはるかに精度が高い。
たとえば、
のように
半ステップだけ進めた値を用いるのである(具体的なことは
常微分方程式のプログラム例を
参考にしてほしい)。
この方法は「改良Euler法」
あるいは「中点法」「Heunの矩形公式」などと呼ばれ、
Euler法に比べるとはるかに精度が高い。
たとえば、
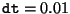 として、
Euler法と改良Euler法の誤差を比べてみよう。
として、
Euler法と改良Euler法の誤差を比べてみよう。
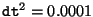 程度だが、
たとえば
程度だが、
たとえば
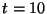 まで
計算しようとすると、1000ステップ分の誤差が蓄積することになる。
蓄積した誤差の大きさは 0.0001 の 1000倍なので 0.1 となり、
たとえば
まで
計算しようとすると、1000ステップ分の誤差が蓄積することになる。
蓄積した誤差の大きさは 0.0001 の 1000倍なので 0.1 となり、
たとえば
 に対して
10%の誤差を生じる。
に対して
10%の誤差を生じる。
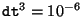 程度なので、
同じく
程度なので、
同じく
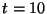 までの計算で
1000ステップ分の誤差が蓄積したとしても、
0.1%の誤差を生じるに過ぎない。
までの計算で
1000ステップ分の誤差が蓄積したとしても、
0.1%の誤差を生じるに過ぎない。
なお「Heunの台形公式」という計算法(単に「Heun法」とも言う)でも、 改良Euler法と同じくらいの精度が得られる。 くわしくは参考文献を見ること。 また間違いプログラムの例(PDF)も参考になるかもしれない。
改良Euler法の基本的な考え方は、 中間的なステップを設けることによって 数値計算の精度を高められるという点にある。 この考えを発展させたのが Runge-Kutta法である。
例として、さっきの方程式(1)の数値解法を考える。 改良Euler法は、少し冗長になるが、次のようにも書ける:
反復 {
v1dt = v(x[j] ) * dt
v2dt = v(x[j] + v1dt/2 ) * dt
x[j+1] = x[j] + v2dt
}
また、Heun法(Heunの台形公式)は次のように書ける:
反復 {
v1dt = v(x[j] ) * dt
v2dt = v(x[j] + v1dt ) * dt
x[j+1] = x[j] + (v1dt + v2dt)/2
}
どちらの場合も、
もしいきなり x[j] = x[j] + v1dt とすれば
Euler法と同じであるが、
そうせずに補助的に v2dt を求めることで精度を高めている。
これにより、累積誤差を
dtの2乗に比例して小さくできる[※]。
改良Euler法やHeun法を総称して「2次Runge-Kutta法」という。
※ 1ステップあたりの誤差は程度であるが、 結果をだすのに必要な全ステップ数は dt に反比例して増えるから、 結果として累積する誤差は dtの2乗に比例する。
単にRunge-Kutta法と言った場合、次のような 4次Runge-Kutta法を指す場合が多い:
反復 {
v1dt = v(x[j] ) * dt
v2dt = v(x[j] + v1dt/2 ) * dt
v3dt = v(x[j] + v2dt/2 ) * dt
v4dt = v(x[j] + v3dt ) * dt
x[j+1] = x[j] + (v1dt + 2*v2dt + 2*v3dt + v4dt)/6
}
4次Runge-Kutta法では、
一定時間のあいだに累積する誤差は dtの4乗に比例する。
2次と4次のどちらが良いかは、場合にもよるので一概には言えないが、
学部の授業における数値計算としては、
まずは2次の方法をきちんと習得することを勧めたい。
本格的な常微分の計算(MDとか天体計算とか)をしたい人は、 牧野先生の「システム数理IV」の講義ノートを読んで勉強するのが良いでしょう。
[このページの冒頭に戻る] [常微分方程式] [微分方程式]