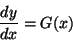 |
(1) |
最終更新日: 2000-11-14
1階微分のみを含む(2階以上の微分を含まない)常微分方程式を考えよう。
うまく式変形して、解ける形にもちこむ。
たとえば
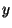 が求められることは
明らかである。
このとき、積分定数として1個の任意定数が生じる。
一般に、 N階の常微分方程式の一般解は
N個の任意定数を含むことが知られている[※]。
1階の常微分方程式の一般解は1個の任意定数を含む。
が求められることは
明らかである。
このとき、積分定数として1個の任意定数が生じる。
一般に、 N階の常微分方程式の一般解は
N個の任意定数を含むことが知られている[※]。
1階の常微分方程式の一般解は1個の任意定数を含む。
※ きわめて特殊な状況で例外が生じることがあるが、ふつうは気にしなくてよい。
式(1)のほかに、 解ける形として、次のようなものがある:
これらの形は、囲碁の定石やマージャンの役と同じように、 見ただけでそれと分かるようにならなければならない。 たくさん練習をつんでしっかりと覚えること。
たとえば
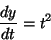
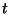 で
積分すれば良いが、
で
積分すれば良いが、
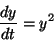
 で積分(?)して
で積分(?)して
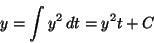
 は
未知の関数なので、
は
未知の関数なので、
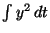 を
簡単に計算するわけにはいかないのである。
今の場合、変数分離にもちこんで
を
簡単に計算するわけにはいかないのである。
今の場合、変数分離にもちこんで
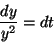
別のよくある間違いは、
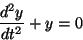
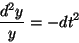
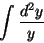
[「定数変化法」に進む] [「常微分方程式」に戻る] [ページの冒頭に戻る]