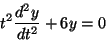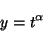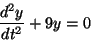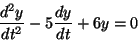
|
(5) |
作成日 : 2000-11-14 / 最終更新日: 2002-05-10
2階微分を含む方程式の場合、 1階の微分方程式とは違った工夫が必要である。
解き方を天下り的に示す前に、
まずは地道に自分の手と頭で考えてみたい。
そのために、1つ具体例を考えてみる(``解き方の見本''という意味ではなく、
いろいろと式をいじって解き方を考えだすための例である)。
たとえば
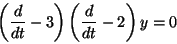
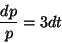
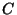 を
任意定数として)
を
任意定数として)
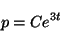
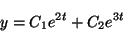 |
(8) |
さて、このようなややこしい手続きをふまずに 一般的に解く方法がないかとは、誰しもが思うことである。 微分方程式(5)がなぜ解けたのか、 よく考えてみると
左辺の微分を``因数分解''できたことが重要であることがわかる。 したがって、一般的に、とにかく 因数分解に持ち込めば解けるのではないかと考えられる。 因数分解ということは、2次方程式と言い替えてもよい。
もうひとつ、微分方程式(5)が
線形微分方程式であることに注目する。
これは、
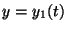 という解と
という解と
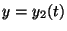 という解が
得られたとき、
という解が
得られたとき、
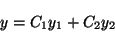 |
(9) |
たとえば
という方程式が
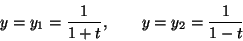
という解をもつことは容易に分かるが(代入して等号成立を確認すればよい)、 だからといって
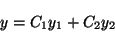
とおいても解にならない(代入して確認せよ)。 方程式(10)は非線形なので、 重ね合わせの原理が成り立たないのである。
話を微分方程式(5)に戻すと、
この方程式は線形であって、重ね合わせの原理が成り立つ。
だから、もとになる解(基本解)
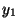 ,
,
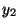 を
とにかく求めれば、
重ね合わせの原理によって一般解が
を
とにかく求めれば、
重ね合わせの原理によって一般解が
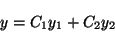
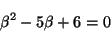
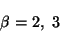
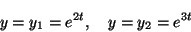
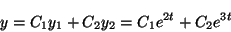 |
(12) |
参考: 基本解について [PSファイル]
このように、微分方程式とは関係ない問題でも、
線形の問題であるならば「基本解」という概念が通用する。
もちろん、
いつでも式(11)のように置けばよいわけではない。
たとえば