定数変化法
最終更新日: 2000-11-14
[「2階の常微分方程式の解き方」に進む]
[「常微分方程式」に戻る]
解ける形の方程式に少しだけ新しい項を追加した形の方程式では、
定数変化法を使うと解ける場合が多い。
たとえば
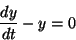 |
(2) |
の一般解は、
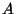 を任意定数として
を任意定数として
と書ける[→ 1階の常微分方程式の解き方を見よ]。
ここで、右辺に新しい項をつけ加えて
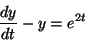 |
(3) |
とした場合の解を考えよう。
右辺がもしゼロなら解はすでに分かっている。
そこで、(無謀かもしれないが)
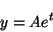 |
(4) |
と置いてみよう。
もちろん、ただ(4)と置いたのでは、
右辺とイコールにすることはできないから、少し工夫し、
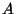 は定数ではなく
は定数ではなく
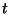 の関数である
の関数である
として式(4)を
微分方程式(3)に代入する。
代入した結果を整理すると
となって、めでたく両辺を
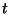 で積分できる形となり、
で積分できる形となり、
すなわち
を得る。
確かに1個の任意定数を含む形であり、
また微分方程式(3)に代入すれば
等号が成り立つことも容易に確認できる。
注意
念のために言っておくと、
何でもかんでも定数変化法で解くのが良いわけではない。
たとえば
のような場合、定数変化法でも解けることは解けるが、
すなおに変数分離に持ち込むほうが良い。
また
のような場合、解を
と仮定して代入するほうが速い(ここで
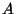 は定数)。
は定数)。
[「2階の常微分方程式の解き方」に進む]
[ページの冒頭に戻る]
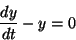
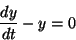
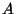 を任意定数として
を任意定数として
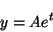
は定数ではなく
の関数である
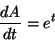
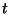 で積分できる形となり、
で積分できる形となり、
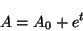
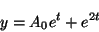
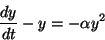
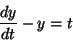
![y = A e^t + [ t の多項式 ]](y=Aet+poly.gif)
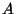 は定数)。
は定数)。