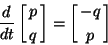 |
(1) |
2000-11-22
注意! 演習室のプリンタの用紙やトナーには限りがあります。 必要以上にたくさん印刷することは避けてください。 特に、WWWの文書(この文書を含む)は、 なるべくオンラインで見るようにしてもらえると助かります。
数値計算にEuler法をそのまま使うと、
dtをものすごく細かくしない限り、
大きな誤差を生じてしまう。
しかし、数値計算法を工夫すれば、精度は劇的に向上する。
たとえば、単振動の方程式
質量 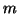 の質点が、
次の3種類の力を受けて、1次元的に運動しているとする:
の質点が、
次の3種類の力を受けて、1次元的に運動しているとする:
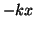
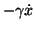
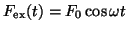
この場合、質点の運動方程式は
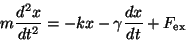
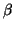 と
と
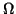 という
2つの無次元パラメータを含んでいる。
という
2つの無次元パラメータを含んでいる。
実験や数値計算の結果を比較する場合には、 無次元パラメータ(今の例ではと
)が 同じであれば、 たとえ
や
が 異なったとしても ``同じ実験条件''と見なすことができる(したがって、たとえば、 減衰が大きいか小さいかを論じる際には、
の大小よりも
の大小で考えるのが正しい)。 なお、本当は初期条件まで合わせてはじめて``同じ実験条件''となるのだが、 初期条件の影響が時間とともに減衰して消え去るような場合には、 初期条件の違いは重要ではない。
ちなみに、式(3)を 式(1)と 同様の形に書き直すと
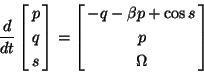
のようになる(ただしを省略した)。 右辺が
を 含まないようにするためには、 式(1)とは違って 変数が3つ必要になることに注意してほしい。 つまり、強制振動の位相空間は3次元である。
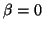 )を考える。
外力の振動数
)を考える。
外力の振動数 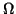 を、
ちょうど共振が起きるような値に設定し、
解
を、
ちょうど共振が起きるような値に設定し、
解 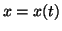 を数値計算で求めて、
を数値計算で求めて、
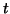 の関数として
図示せよ。
初期条件は10月の課題[1]と同じとする。
また、同じ条件に対する解を手計算で求め、
数値計算の結果と一致することをグラフにより確認せよ。
の関数として
図示せよ。
初期条件は10月の課題[1]と同じとする。
また、同じ条件に対する解を手計算で求め、
数値計算の結果と一致することをグラフにより確認せよ。
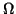 の値を、
ちょうど
の値を、
ちょうど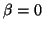 で
共振が起きるような値に設定する。
微小な減衰(
で
共振が起きるような値に設定する。
微小な減衰(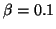 )が存在する場合について、
系が定常状態に達するまで数値計算をおこない、
解を
)が存在する場合について、
系が定常状態に達するまで数値計算をおこない、
解を 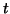 の関数として図示せよ。
この結果を、
の関数として図示せよ。
この結果を、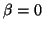 の場合と比較せよ。
なお、初期条件は好きなように選んでよい。
の場合と比較せよ。
なお、初期条件は好きなように選んでよい。
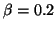 とする。
外力の振動数
とする。
外力の振動数
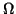 の値を
さまざまに変えて数値計算をおこない、
横軸に
の値を
さまざまに変えて数値計算をおこない、
横軸に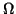 ,
縦軸に定常応答の振幅をとってグラフにまとめよ。
また、定常振幅と
,
縦軸に定常応答の振幅をとってグラフにまとめよ。
また、定常振幅と 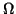 のあいだの関係式を理論的に求め、
数値計算の結果と一致することを確認せよ。
のあいだの関係式を理論的に求め、
数値計算の結果と一致することを確認せよ。
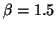 として、課題[2]と同様に
さまざまな
として、課題[2]と同様に
さまざまな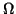 に対する定常応答振幅を求め、
理論と比較せよ。
に対する定常応答振幅を求め、
理論と比較せよ。
これらの課題をレポートにまとめ、 12月18日の朝までに 事務室前のレポート箱に提出すること。