2001-01-10 作成 / 2001-01-23 一部訂正
ふたつの振り子がバネで結ばれている系の運動方程式を書き下そう。
具体的にどのような系なのかについては、 本日配布したプリントにある模式図か、 12月6日「多自由度の振動(2)」の課題プリントを見てほしい。支点
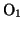 を原点にとり、
を原点にとり、
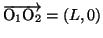 とする。
単位ベクトル
とする。
単位ベクトル
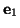 および
および
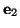 を
を
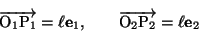
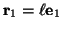 ,
,
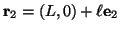 であり、
その他の力についても適当に記号を定義すれば、
運動方程式はベクトル形で
であり、
その他の力についても適当に記号を定義すれば、
運動方程式はベクトル形で
![m (d/dt)^2 r1 = - T1 e1 + mg + f[2->1];
m (d/dt)^2 r2 = - T2 e2 + mg + f[1->2]](EqM_pend2.gif)
のように書ける。
この式から
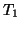 および
および
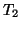 を消去して整理すればよい。
を消去して整理すればよい。
上記の運動方程式において、と
は、 振り子の糸(または針金)を通じて質点に及ぼされる力の大きさであり、 この力の向きは
および
によって決まる。 これは、以前に「力学演習I 課題(5): 束縛運動」や 「力学演習I 課題(10): 剛体の力学の基礎」、 「力学演習II 剛体の力学(2)」などで既に学んだ内容なので、 自信のない人はこの機会に復習しておくこと。
また、質点P1と質点P2は、 バネを介して相互作用している。 バネの力の取り扱いについても何度か学んできたわけであるが、 特に「力学演習I 課題(8): 衝突と2体問題」 および「力学演習 課題(9): 惑星の運動」を参考にすると良いだろう。
途中の計算は省略するが、微小振幅の場合には、
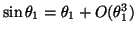 などの近似を用いて
などの近似を用いて
振幅が大きい場合には このような近似はできないので、
近似なしで計算してみると
![xi = sqrt[ 1 + 2R(sin(θ2)-sin(θ1)) + 2 R^2 ( 1-cos(θ2-θ1) ) ]](xi=.gif) ,
,
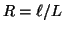 である。
である。
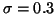 とし、
初期条件を
とし、
初期条件を
![θ1[t=0] = 0.1](ini_th1=01.gif) ,
,
![θ2[t=0] = 0](ini_th2=0.gif) ,
,
![(d(θ1)/dt)[t=0] = (d(θ2)/dt)[t=0] = 0](ini_dt=0.gif) と
したときの解を手計算で求め、
GNUPLOTを用いて、
と
したときの解を手計算で求め、
GNUPLOTを用いて、
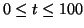 の範囲でグラフ化せよ。
の範囲でグラフ化せよ。
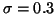 ,
,
![θ1[t=0] = θ2[t=0] = 0.1](ini_th=01.gif) ,
,
![(d(θ1)/dt)[t=0] = (d(θ2)/dt)[t=0] = 0](ini_dt=0.gif) としたときの
解を求め、グラフ化せよ。
としたときの
解を求め、グラフ化せよ。
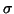 が小さい場合
(たとえば
が小さい場合
(たとえば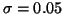 )について
数値計算をおこない、
それぞれの振り子のエネルギーの時間変化をグラフ化せよ。
また、系全体のエネルギーが保存されていることを示せ。
)について
数値計算をおこない、
それぞれの振り子のエネルギーの時間変化をグラフ化せよ。
また、系全体のエネルギーが保存されていることを示せ。
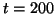 程度まで計算し、
エネルギーが確かに一定値になることを確認すること。
パラメータの値は
σ=1.0, R=0.5に固定し、
程度まで計算し、
エネルギーが確かに一定値になることを確認すること。
パラメータの値は
σ=1.0, R=0.5に固定し、
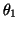 ,
,
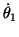 ,
,
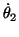 の初期条件もゼロに固定して、
の初期条件もゼロに固定して、
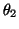 のみについて
のみについて
![θ2[t=0] = 0.1, 0.101, 0.6, 1.1, 1.101](ini_th2=01-11.gif) のように
初期条件を変化させること。
結果が得られたら、
線形方程式(1)(2)の結果と比較せよ。
のように
初期条件を変化させること。
結果が得られたら、
線形方程式(1)(2)の結果と比較せよ。
これらの課題をレポートにまとめ、 2月5日の朝までに 事務室前のレポート箱に提出すること。