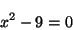 |
(1) |
2002-05-10 更新 / 2008-06-22 微更新
失礼ながら少々お尋ねしますが、まさか
宿題の答えを探しに来られたわけではないですよね??
もしそうであるなら、以下の内容を参考にするまえに、
宿題を出した先生の意図は何であるかを
ちょっと考えてみてください。
そのうえで、その意図にそった形で
当ページの内容を利用していただければと思います。
参考: 「教えて! goo」に宿題を頼む前に考えてほしいこと
[「微分方程式」に戻る] [物理の部屋に戻る]
個人的な意見ではあるが、 応用数理工学科の講義のメインテーマは 微分方程式が解けるようになることだと私は思っている。 歴史をたどるなら、そもそも宇宙の法則を解明するために ニュートンやライプニッツが編み出した方法が、微分方程式であったのだ。 微分方程式には、大きく分けて常微分方程式と偏微分方程式があり、 どちらも数学を現実の世界に応用するうえできわめて重要である。
まず「方程式とは何か?」と言えば、それは「未知数を含む等式」であり、
くわしく言うと「未知数に何か特定の値を代入したときに限って
成り立つようになっている等式」のことである。
たとえば
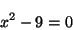 |
(1) |
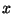 に
任意の値を代入したのではだめで、
に
任意の値を代入したのではだめで、
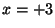 とか
とか
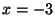 とかいう
特定の値を
とかいう
特定の値を
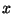 に代入したときに限って
等号が成り立つ。
等号を成り立たせるような
未知数
に代入したときに限って
等号が成り立つ。
等号を成り立たせるような
未知数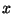 の値を
求めることが、すなわち``方程式を解く''ことである。
の値を
求めることが、すなわち``方程式を解く''ことである。
微分方程式は、微分を含む方程式である。
ただし、ふつうの方程式とは違って、未知数を求めるのではなく、
未知の関数を求めることになる。
たとえば
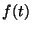 を求めよ、というのがその例である。
を求めよ、というのがその例である。
ちなみに、微分方程式(2)の一般解は、,
を任意定数として
である。
物理学の法則や工学的な数理モデルは、 微分方程式の形であらわされることが多い。 なぜかというと、 微分とは「変化を数学的にあらわしたもの」だからである。 したがって、何か変化するものを予測しようという場合には、 ほとんど必ず微分方程式が関係してくると言ってよい。
微分方程式のなかには、
1変数関数を扱う常微分方程式(ODE)と、
多変数関数を扱う偏微分方程式(PDE)がある。
たとえば
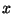 と
と
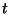 の
2つであるから、
これは偏微分方程式(PDE = Partial Differential Equation)である。
つまり、
の
2つであるから、
これは偏微分方程式(PDE = Partial Differential Equation)である。
つまり、
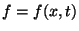 という
2変数関数を求めなければならない。
偏微分方程式を解くのは、常微分方程式に比べてはるかに難しい。
という
2変数関数を求めなければならない。
偏微分方程式を解くのは、常微分方程式に比べてはるかに難しい。
これに対して、
たとえば、さっきの微分方程式(2)は、
独立変数が 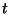 だけなので
常微分方程式(ODE = Ordinary Differential Equation)である。
また
だけなので
常微分方程式(ODE = Ordinary Differential Equation)である。
また
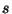 だけなので
常微分方程式である(従属変数
だけなので
常微分方程式である(従属変数
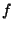 ,
,
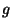 に関する
連立常微分方程式になっている)。
に関する
連立常微分方程式になっている)。
物理の例を挙げると、質点力学にでてくる Newtonの運動方程式は常微分方程式であるが、 Navier-Stokes方程式やMaxwell方程式は偏微分方程式である。 量子力学のSchro"dinger方程式は 偏微分方程式であるが、 1粒子1次元系の定常状態のような特別な場合には、 常微分方程式に直して解くことができる。
常微分方程式の本はたくさんあるが、 私(大信田)が持っている本のなかから2冊だけ挙げておく。 あとで追加するかもしれない。
なお、数値計算についてのリンク集も参照。
[このページの冒頭に戻る] [微分方程式] [物理の部屋]